Since Linear Increase of the form: P_t = P₀ + m t

Point #1 (t, P) = 2, 25.1) and Point #2 = (10, 25.5)

First find 

P₀: Using point #1: 25.1 = P₀ + 0.05 (2), P₀ = 25 millions

So the initial population was 25 millions

(linear formula is P = 25 + 0.05 t )

Question 2. The value of a new car purchased in 1995 depreciates linearly from $16,500 to
$14000 after 5 years, what is the rate of depreciation of the car in $ per year?

Rate of depreciation is a decreasing function so rate m is negative:

( formula would be: P = 16,500 - 500 t)

Question 3. Number of students, N, attending Ridgemount Community College increases
at a constant rate over a 4 year period. From the graph shown below write a formula for
Number of Students as a function of year, t since 1985.
 
 

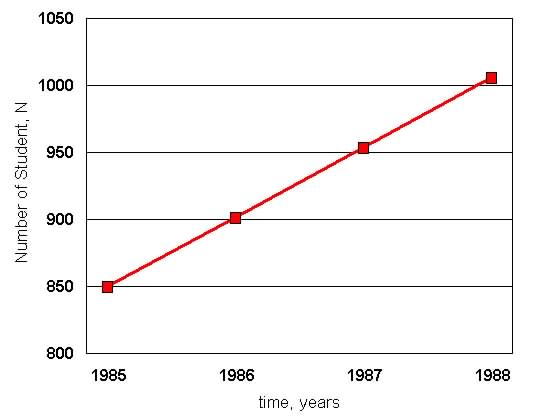Point 1: (1985, 850)

Point 2: (1988, 1006)

Linear Growth so formula is : N_t = b + m t

Find m: using 1988 and 1985 data: 

Since b = 850 (Number of students at time = 0, 1985) formula is N_t = 850 + 52 t

Question 4. The cost of yearly tuition, C in $ for students at Ridgemount Community College increases
at a constant rate over a 4 year period. From the information shown in the table below write a formula
for yearly tuition cost as a function of time, t in years since 1985.

C = 3206 + 105 t

Year, t	Number of Students, N	Tuition Cost per year for students, C, $
1985	850	3,206
1986	902	3,311
1987	954	3,416
1988	1,006	3,521

Linear Growth so formula is : C_t = b + m t

Find m: using 1988 and 1985 data: 

Since b = 3206 (Tuition at time = 0, 1985) formula is C_t = 3,206 + 105 t

Question 5. The population, P_t, millions, of a country was observed the second year at 10.1 millions
and 11.5 millions the tenth year, where t is years. What was the initial population of this country
when it was observed if it grows linearly?

Since Linear Increase of the form: P_t = P₀ + m t

First find 

P₀: Using point #1: 10.1 = P₀ + 0.175 (2), P₀ = 9.75 millions

So the initial population was 9.75 millions

Question 6. The value of a farm equipment purchased in 1987 depreciates linearly from $20,000 to
$16,250 after 5 years, what is the rate of depreciation of the equipment per year?

Rate of depreciation is a decreasing function so rate m is negative:

( formula would be: P = 20,000 - 750 t)

Question 7. The value of a new car purchased in 1990 depreciates linearly from $18,500 to $16,000
after 5 years, write a formula for the depreciation of the car as a function of time in year?

Since V₀ = 18,500, V_t = 18,500 - 500 (t)

Question 8 A woodworker goes into business selling carved wooden horses; if the total cost,
C in $ for carving n horses is shown in the table below: write a formula that shows
the cost as a function of n horses:

n, number of horses	C, total cost ($)
1	5350
2	5700
5	6750
10	8500

Linear since rate: 

So cost at n = 0: Using (1, 5350): 

So formula: C = 5000 + 350 (n) (check when n = 10: C = 5000 + 350(10)=8500)

Question 9. Find the formula for the linear depreciation of the value of an automobile
from $25,000 to $20,450 in 7 years. V = b + m(t) (linear model)

At t = 0, b = $25,000 (start time of depreciation)

So