Department of Mathematics Theory

Precalculus  by Example Series Exponential  and Logarithm Functions

Question 1. When will the number of people infected with a certain virus be reduced
to ½ its its current number if its is decreasing at a rate of 0.3 % each day?, therefore,
r=0.003

Let Number infected with time be P_t, then 

When number infected is ½ , P_t = ½ P₀ =P₀(0.997)^t

Divide through by P₀: ½ = (0.997)^t

Take logs (ln) of both sides: ln ( ½ ) = t ln(0.997),

So 

(check: P_230.7=P₀(0.997)^230.7 = P₀ x 0.5 = ½ P₀)

Question 2. What will be the population of doves after 10 years if the current population
is 61,000 and expects to grow exponentially at a rate of 0.005 % each year?

Since exponential growth: P_t =P₀ (1+r)^t , r = 0.005 / 100 = 0.00005, t = 10

P_t =61,000 (1+0.00005)¹⁰ =61030.5 or 61,031

Question 3. The cost of tuition per year, C, for students attending Ridgemount Community College increases at a constant percent rate (so exponential) over a 4 year period since 1985. From the information shown in the table below:
 

Year, t	Number of Students, N	Tuition Cost per year for students, C, $
1986	Not Available	3,238.06
1987	867	3,270.44
1988	Not Available	3,303.15
1989	885	3,336.18

(a) Write a formula for Yearly Cost of Tuition, C, as a function of year, t since 1985.

(note t = 0 is 1985, t=1 is 1986) C=3206(1.01)^t

Given t=2, C₂ =3270.44 and t =4. C₄ = 3336.18, So C_t=C₀ (1+r)^t

C₀ = $3,206

Question 4. An investment grows at a rate of 3% each year. How long will it take
the investment to double its value?

Let Investment with time be I_t, then

When Investment doubles I_t = 2 I₀ =I₀(1.03)^t

Divide through by I₀: 2 = (1.03)^t

Take logs (ln) of both sides: ln (2) = t ln(1.03),

So 

(check: I_23.45=I₀(1.03)^23.45 = I₀ x 2 = 2 I₀)

Question 5. What will be the population of doves after 5 years if the current population
is 60,500 and expects to grow exponentially at a rate of 0.009 % each year?

Since exponential growth: P_t =P₀ (1+r)^t , r = 0.009 / 100 = 0.00009, t = 5

P_t =60500 (1+0.00009)⁵ =60527.23 or 60,527

Question 6. Number of students, N, attending Ridgemount Community College
increases at a constant percent rate (so exponential) over a 4 year period since 1985.
From the information shown in the table below:
 

Year	Number of Students, N	Tuition Cost per year for students, C, $
1986	Not Available	3,238.06
1987	867	3,270.44
1988	Not Available	3,303.15
1989	885	3,336.18

(a) Write a formula for Number of Students as a function of year, t since 1985.
(note t = 0 is 1985, t=1 is 1986) N=850(1.01)^t

Given t=2, N₂ =867 and t =4. N₄ = 885 function is: N(t) = N₀ ( 1+r)^t

N₀ = 849 or 850 students

So N(t) = 850 ( 1.01)^t

(b) State the percent growth rate and the Number of students in 1985.

Rate is 1.03 % and N(1985) is about 850

Question 7. When will a population growing at 2.5% each day doubles in size?

28.07 days

t = 28.07 days

Question 8. When will two populations be equal in size if one population starts at 100 thousands
and grows each year by 3.5% and the other population starts at 50 thousands and grows each year by 5%?

and  both functions intersect in t = 48.17 years

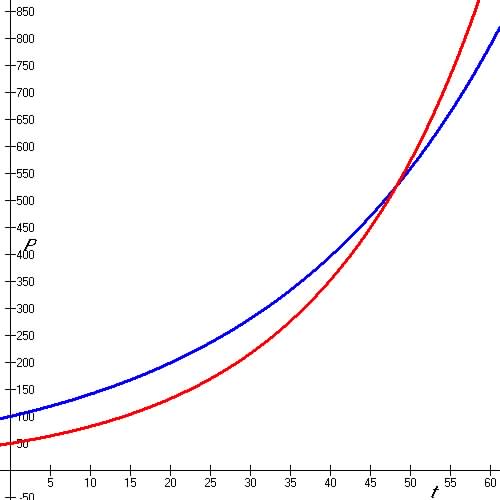Take ln of both sides:

48.17 years

Question 9. A radioactive substance decays exponentially to 1/3 its original weight after 6 hours,
how much will be left after one day?

First determine the rate of decay, r or (1-r): let W = weight of substance

W₀ cancels out:

so 

After 1 day or 24 hours:

Question 10. What is the interest gained on $50,000 on gold deposited in a bank for 2 years
and compounding interest daily at an annual rate of 6% ?

=$56.374.29 So interest = P(2) - 50,000 = $6,374.29

Question 11. A population size 2 years after it was observed is 70.93 millions and
74.67 millions after the 4th year. Assuming exponential growth write a formula for
the population size P as a function of time, t in years since observed.

Exponential growth: 

Find (1+r): 

Find P₀: Using P₂: 70.83=P₀(1.02675)²=P₀(1.0542), P₀= 67.19 millions

So P_t = 67.19 (1.02675)^t