Using Law of Sines to find B: .7377

=> B = sin ^-1 = 47.54⁰ So C = 180 - (40.2 + 47.54) = 92.26⁰

Using Law of Sines to find c: 
 
 

A=40.20 B=47.540 C= 92.260 A=7ft, b=8ft and c=10.84 ft

Question 2. Find all solutions to  in interval 

=> 30⁰ and -30⁰ for cos (-)

 
 

So

Question 3 - Given that the  in the 4th quadrant: Find:

(a)  (b)  (c)

In Q-IV: 

So 

(a)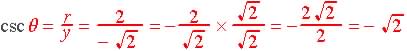 

(b) 

(c) 

Question 4. Find all solutions to 3 in the interval

19.47⁰ tan is also (+) in Q-III so 180+19.47 is also a solution: 199.47⁰

So solutions 

Question 5 - A kite flyer wondered how high her kite was flying.
She used a protractor to measure an angle of 38⁰ from level ground
to the kite string. If she used a full 100 yard spool of string, how high, in feet,
was the kite ? (disregard the string sag and height of the reel above the ground).

Given A = 38⁰, hyp = 100 yds or 100 x 3 = 300 feet: Find opposite side:

Question 6. Solve the following triangle: B = 135 deg 4 min, a= 3 cm
and c = 5 cm. B = 135 + 4/60 deg = 135.06667

Law of cosines: Find side b: =55.2379

Law of Sines to find A: 0.2851

A => 16.56⁰ [sin^-1 (0.2851)]

So C = 180 - (135.07 + 16.56) = 28.23⁰
 
 

A = 16.560 C = 28.230 b = 7.4322 cm

Question 7. Find all solutions to  in interval 

Since 

Use identity with sin(x):

Substitute: 

: let 

So: 

Replace 

So (a)  sin also (+) in Q-II therefore 

(b) or  sin also = 0 at 180⁰
 
 

Question 8. Find all solutions to  in interval 

Since 

Then 

So: 

Or: