5.
Number Theory
5.1 Primes, Composites, and Tests
for Divisibility
Counting Numbers:
1,
2, 3, 4, 5, 6, .......
Prime Numbers:
Divisable
by itself and 1: 2,
3, 5, 7, 11, 13 , 17, 19, ...
Composite
Numbers: at least 3 factors - e.g. 60 =
2 x 2 x 3 x 5
a | b means a divides b (quotient is a whole number)
| Theorem:
Fundamental
Theorem of Arithmetic - Each
Composite number can be a factor of prime numbers
-
e.g. 60 = 2 x 2 x 3 x 5 |
Theorem:
Test
for divisibility by 2, 5 & 10 -
Number divisible by 2
if ends in 0 or even digit
Number divisible by 5
if ends in 0 or 5
Number divisible by 10
if ends in 0 |
| Theorem:
Let
a, m, n be whole numbers -
If a | m & a | n, then a | (m+n)
If a | m & a | n, then a | (m-n) for m n
If a | m, then a | km (multiple of ) |
Theorem:
Test
for divisibility by 4 & 8 -
Number divisible by 4 if
last 2 digits divisible by 4
Number divisible by 8 if
last 3 digits divisible by 8 |
| Theorem:
Test
for divisibility by 3 & 9 -
Number divisible by 3 if
sum of digits divisible by 3
Number divisible by 9 if
sum of digits divisible by 9 |
Theorem:
Test
for divisibility by 11 - Number
divisible by 11 if ( sum
of digits in even positions)
- (sum of digits in odd positions)
divisible by 11
e.g. 909381=>(9+9+8)-(0+3+1)=22 is / 11 |
| Theorem:
Test
for divisibility by 6 -Passes
tests for divisibility by 2 & 3
Theorem: Product
divisibility - Number divisibility
by both a & b, then a & b has
1
as common factor |
Theorem:
Prime
Factor Test - Test if n
is prime: see if primes up to p is divisor of n: where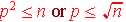 
Is 299 a prime ?
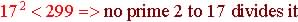 So
299 is a prime
|
5.2 Counting factors, Greatest
Common Factor (GCF)
& Least Common Multiple
(LCM)
Theorem: Counting
Factors - If counting number expressed
as product of distinct primes:
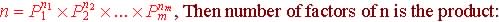
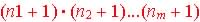number
of factors for 144=24 x 32=> (4+1)(2+1)=15
Greatest Common Factor (GCF):
The
GCF of 2 or
more whole numbers is the largest whole number
that is a factor of both (all)
1. Prime Factor
Method: The product of highest prime common
to both (all):
e.g. GCF(24, 36): 24= 23 x 3 and
36=22 x 32 so GCF=>
22x3 = 12
2. GCF Theorem
Method: GCF(a,b) = GCF(a-b, b) when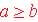 
:
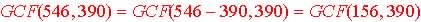
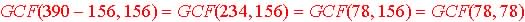
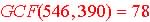
3. Remainder
Method: Theorem: GCF(a, b) = GCF(r,
b):
If a & b are whole
numbers and a >= b and a = kb + r , where r < b
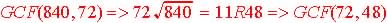
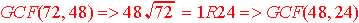
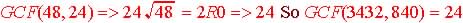
Least Common Multiple (LCM):
The
LCM of 2 or
more whole numbers is the smallest whole number
that is a multiple of each (all) of the numbers.
1. Set Intersection
Method: Smallest element of the intersection of multiple
of the set of each numbers:
e.g. LCM(24, 36): 24= {24,48,72,96,120,144..}
36={36,72,108,144..}= {72, 144} So LCM(24,
36) = 72
2. Prime Factor
Method: The product of largest prime exponent in each (all):
e.g. LCM (24, 36): 24= 23x 3 and
36=22 x 32 so GCF=>
23x32 = 72
3. Buildup
Method: State all prime, select prime of one number and build
up to largest exponent:
e.g. LCM(42, 24): 24= 23 x 3 and
42=23 x 3 x 7 so LCM(42,24)= 23x3x7
= 168
GCF and LCM - Theorems
Theorem: GCF & LCM: GCF(a,
b) x LCM (a, b) = ab
For example, find LCM
(36,56) if GCF(36,56)=4
LCM x GCF = 36 x 56, So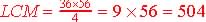 
Theorem: Infinite Number of Primes:
There
is an infinite number of primes
Algorithm for primes:
Sieve of Eratosthenes
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| 31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
| 41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
| 51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
Directions: Skip the number 1, circle 2 and cross out evry second
number after 2,
Circle 3 and cross out every 3rd number after 3 (even if it had
been crossed out before).
Continue this procedure with 5, 7, and each succeeding number not
crossed out.
Circled numbers are primes and crossed out numbers are compsites.