Chapter 6.1 Systems of Linear Equations

Pindling College Algebra   by Example  Series

Key Concepts: Solve systems of linear equations using various techniques

Skills to Learn.

1. Know how to solve systems of 2 linear equations using :

(a) Graphical Method

(b) Substitution Method

(c) Addition Method (also called Elimination )

2. Know how to recognized systems with no solution (inconsistent system)

3. Know how to solve systems with infinitely many solutions

4. Know how to solve system with 3 linear equations

Example 1 - Solve 2 linear equations simultaneously

(1)

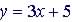
(2)

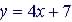
By Substitution Solve for y in terms of x in equation (1) , now replace for y in equation (2) (2b) , group x terms and solve for x Substitute x = -2 in equation (1) to find y So solution is x = -2 and y = -1 or (-2, -1)	By Addition (or Elimination) Eliminate a variable, y by multiplying equ (2) by -1 and adding to equation (1) (1 ) (2a) , So (1) + (2) = Substitute x = -2 in equation (2) to find y (2) So solution is x = -2 and y = -1 or (-2, -1)
By Graphical Solution.

Example 2. Solve

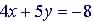
(1)	(3)
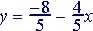
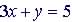
(2)	(4)

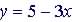
By Substitution Solve for y in terms of x in equation (2) , now replace for y in equation (1) (1b) , group x terms and solve for x Substitute x = 3 in equation (2) or (4) to find y So solution is x = 3 and y = - 4 or (3, -4)	By Addition (or Elimination) Eliminate a variable, y by multiplying equ (2) by - 5 and adding to equation (1) (1 ) (2a) , So (1) + (2) = Substitute x = 3 in equation (2) or (4) to find y (2) So solution is x = 3 and y = -4 or (3, -4)
By Graphical Solution. Plot equ (3) and (4)

Example 3. Solve

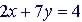
(1)	(3)
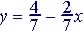
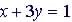
(2)	(4)

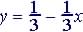
By Substitution Solve for x in terms of y in equation (2) , now replace for x in equation (1) (1b) , Substitute y = 2 in equation (1) to find x So solution is x = -5 and y = 2 or (-5, 2)	By Addition (or Elimination) Eliminate a variable, x by multiplying equ (2) by - 2 and adding to equation (1) (1 ) (2a) , So (1) + (2) = Substitute y = 2 in equation (2) or (4) to find y (2) So solution is x = -5 and y = 2 or (-5, 2)
By Graphical Solution. Plot equ (3) and (4)

Example 4. Solve

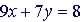
(1)	(3)
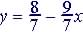
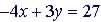
(2)	(4)

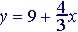
By Substitution Solve for x in terms of y in equation (2) , now replace for y in equation (1) (1b) , Substitute x = -3 in equation (1) to find y So solution is x = -3 and y = 5 or (-3, 5)	By Addition (or Elimination) Eliminate a variable, y by multiplying equ (1) by 4 and equ (2) by 9 and add both (1a ) (2a) , So (1) + (2) = Substitute y = 5 in equation (2) or (4) to find y (2) So solution is x = -3 and y = 5 or (-3, 5)
By Graphical Solution. Plot equ (3) and (4)

Example 5. Infinitely many solutions

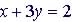
(1)	(3)
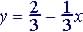
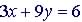
(2)	(4) , same equations so infinitely man solutions since line overlap

By Substitution Solve for x in terms of y in equation (2) , now replace for y in equation (1) (1b) , 0 = 0, No values for y and equation (3) = equation (4) so same line. Infinite solution

By Addition (or Elimination) Eliminate a variable, y by multiplying equ (1) by -3 and add both together (1a ) (2a) , So (1) + (2) = 0 = 0, No values for y and equation (3) = equation (4) so same line. Infinite solution

Example 6. Inconsistent System - no solution

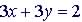
(1)	(3)
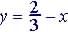
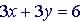
(2)	(4) 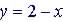, same slope so parallel lines - will never meet

By Substitution Solve for x in terms of y in equation (2) , now replace for y in equation (1) (1b) , inconsistent solution since No Solution	By Addition Eliminate a variable, y by multiplying equ (1) by - 1 and add both together (1a ) (2a) , So (1) + (2) = , inconsistent solution since No Solution
Graphic Solution