Chapter  5.1 Synthetic Division of Polynomials

Pindling College Algebra   by Example  Series

Key Concepts: Division of Polynomials by a linear function represented by its roots (x + r) and theorems related to
divisions, roots and remainder or polynomial division

Skills to Learn.

1. Know how to divide a polynomial by a linear function of the form (x - r)

2. Know how to perform synthetic divisions of polynomials

3. Know how to determine the remainder of a polynomial division

4. Know the remainder theorem

5. Know how to find the roots of a polynomial

Division Algorithm  (Programs, Worksheets, and Animation) For polynomial, P(x) of degree greater than 0 and a real number r, there exist a unique polynomial, Q(x) of degree 1 or less than P(x) and a unique number R such that P(x) = (x - r)Q(x) + R The polynomial Q(x) is called the quotient, (x - r) is the divisor, and R is the remainder. R can = 0; when R = 0, r is a root of the Polynomial P(x), i.e. P(r) = 0

Example 1. P(x) = 2x2 + 4x + 5 divided by (x + 2) gives: P(x) = 2x2 + 4x + 5 = (x - (-2))(2x + 2) + R = (x + 2)(2x) + 5

Synthetic Division

Synthetic Division Process: To divide the polynomial P(x) by (x - r) Step 1: Arrange the coefficients of P(x) in order of descending powers of x. Write 0 as the coefficient for each missing power. Step 2: After writing the divisor in the form (x - r), use r to generate the 2nd and first rows as: 2nd & 3rd rows: Place r in the first column of the 3rd row Bring down the first row coefficients to the 3 row Multiply the coefficient brought down by r and place in 2nd row Add this product to the 1st row's coefficient of the dividend and place in 3rd row Multiply this 3rd row addition by r and place in 2nd row Repeat until a product is added last column of the 3rd row is filled in Step 3: The last number in the 3rd row is the remainder of the division. The other numbers in the 3rd row is the coefficient of the quotient, which is of degree 1 less that of P(x)

Example 2 Divide by . Variable of P(x) r             Coefficient P(x)   4 0 -30 0 -50 -2 2nd row     -12 36 -18 54 -12 Coefficient Q(x) -3 4 -12 6 -18 4 -14 Variable of Q(x)             R Dividend is (x - (-3)) = (x + 3), r = -3 Remainder (R) is -14 or P(-3) = -14 Quotient, Q(x) is - P(r) = (x - r)Q(r) + R

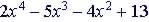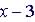Example 3 Divide by . Variable of P(x) r           Coefficient P(x)   2 -5 -4 0 13 2nd row     6 3 -3 -9 Coefficient Q(x) 3 2 1 -1 -3 4 Variable of Q(x)           R Dividend is (x - 3), r = 3 Remainder is 4 or P(3) = 4 Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

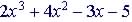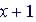Example 4 Divide by . Variable of P(x) r         Coefficient P(x)   2 4 -3 -5 2nd row     -2 -2 5 Coefficient Q(x) -1 2 2 -5 0 Variable of Q(x)         R Dividend is (x + 1), r = -1 Remainder is 0 or P(-1) = 0. When remainder is 0, r is root of P(x), so -1 is root of P(x) Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

Example 5 Variable of P(x) r               Coefficient P(x)   1 7 10 0 -1 -5 0 2nd row     -5 -10 0 0 5 0 Coefficient Q(x) -5 1 2 0 0 -1 0 0 Variable of Q(x)               R Dividend is (x + 5), r = -5 Remainder is 0 or P(-5) = 0. When remainder is 0, r is root of P(x), so -5 is root of P(x) Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

Example 6 Variable of P(x) r           Coefficient P(x)   2 9 5 -4 3 2nd row     -3 -9 6 -3 Coefficient Q(x)   2 6 -4 2 0 Variable of Q(x)           R Dividend is Remainder is 0 or P(-5) = 0. When remainder is 0, r is root of P(x), so -1.5 is root of P(x) Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

Example 7 Variable of P(x) r           Coefficient P(x)   1 0 0 0 -16 2nd row     -4 16 -64 256 Coefficient Q(x) -4 1 -4 16 -64 240 Variable of Q(x)           R Dividend is Remainder is 0 or P(-4) = 240. Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

Example 8 (remember that and ) Variable of P(x) r           Coefficient P(x)   1 2 -2 2 -3 2nd row     i 3 Coefficient Q(x) i 1 2 + i     0 Variable of Q(x)           R Dividend is Remainder is 0 or P(i) = 0. When remainder is 0, r is root of P(x), so is root of P(x) Quotient, Q(x) is in form: P(r) = (x - r)Q(r) + R

Try this problem: ; the answer is the same as above example 8.