Chapter  4.3 Logarithmic Functions and Their Graphs

Pindling College Algebra   by Example  Series

Key Concepts: Logarithmic functions, their relationship to exponential functions and graphs of logarithmic functions

Skills to Learn

1. Know that the inverse of exponential functions are logarithmic functions and visa versa

2. Know how to compare and convert between logs and exponential

3. Know how to perform calculations in the Base-10 or Base-e Logarithms scales

4. Know the basic properties of logarithms

5. Know how to graph logarithmic functions

6. Know how to transform logs: vertical and horizontal shifts

Logarithms (logs) or inverse functions of exponential and Exponential functions are inverse functions of logarithms

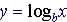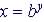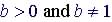
For the function , its inverse function is , if is the exponent by which the base, b is raised to get x When b = 10: the functions becomes , its inverse function is , this logarithm function is called the common logarithm function and is called the Base-10 log function. When b = e: the functions becomes , its inverse function is , this logarithm function is called the natural logarithm function and is called the Base-e log function.

Logs	Exponents	Solution for y
logb x = y	x = b y	y
log2 8 = y	8 = 2 y	3
log5 125 = y	125 = 5 y	3
log10 10,000 = y	10,000 = 10 5 = 10 y	5
log10 (1/100) = y	1/100 = 10 -2 = 10 y	-2

Example: Find a for loga 25 = 2 Convert to exponent form: 25 = a 2,

Example: Find a for log64 a = ½ Convert to exponent form: a = 64 ½ ,

Example: Find a for loga 1 = 0 Convert to exponent form: 1 = a 0, a is any real number

Base - 10 Conversions

Logs	Exponents	Solution for y
log10 x = y	x = 10 y	y
log10 1 = y = 0	1 = 10 y = 10 0	0
log10 10 = y = 1	10 = 10 y = 101	1
log10 100 = y = 2	100 = 10 y = 102	2
log10 10 n = y	10 n = 10 n	n
log10 (1/10) = y	10 -1 = 10 y	-1
log10 (1/100) = y	10 -2 = 10 y	-2
log10 10 -n = y	10 -n = 10 y	-n

Properties of Logs:

Note: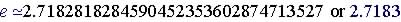

Common log	Example	Natural log	Example
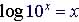
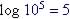
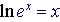
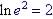
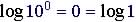
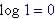
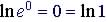
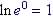
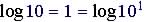
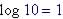
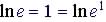
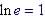
Domain 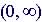Range		Domain 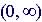Range

Solve Log Problems:

Example. Solve log x = 1.25 Convert the exponential x = 10 1.25 = 17.7828 Check log (17.7828) = 1.25	Example. Solve ln x = 10 Convert the exponential x = e 10 = 22026.4658 Check ln (22026.4658) = 10
Example write the value of e to 13 decimal places using your calculator. Since ln e = 1 Convert the exponential e = e 1 = 2.7182818284590	Example. Solve the equation: for x See instructor when you find solution if not asked

Graphing Logarithmic functions (create table of point (x, y) and note this is always true (1, 0)

Example. Graph 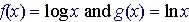on the same graph	Example . Graph 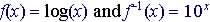on the same graph (note their line of symmetry, y = x)
Example. Graph 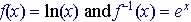on the same graph (note their line of symmetry, y = x)	Example. Graph 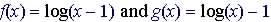on the same graph (note f(x) is a horizontal shift and g(x) is a vertical shift)

Transformation of Logarithmic Functions

(Vertical and Horizontal shifts)

Given the exponential function 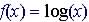Horizontal transformation occurs when h is introduced in the function in this manner: , when h is positive the functions is shifted to the right by h units and : when h is negative, the functions is shifted to the left by h units Vertical transformation occurs when k is introduced in the function in this manner: , when k is positive the functions is moves upward by k units and : when k is negative the function moves down by k units

Example. Horizontal Shifts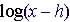

Example. Vertical Shifts
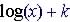