Chapter  4.1 Exponential Functions and Their Graphs

Pindling College Algebra   by Example  Series

Key Concepts: Fundamental properties of Exponential Functions and their graphs

Skills to Learn:

1. Know about rational and irrational exponents of exponential functions

2. Know how to recognize exponential functions and graph them

3. Know how to calculate applications of exponential functions involving compounding

4. Know the relationship between periodic and continuous compounding

5. Know how to transform exponential functions: vertical and horizontal Shifts

Exponential Functions: With rational and irrational exponents

Exponential functions are functions of the form: , where x can be any real number and b any positive number except 1 Exponential functions can have both rational and irrational exponents

Example 1 - An increasing (i.e. The coefficient of x is positive or b greater than 1) Exponential Function with a rational exponent Increasing Functions: as x get large, y gets larger also

Example 2 - A decreasing (i.e. The coefficient of x is negative or b less than 1) Exponential Function with a rational exponent Decreasing Functions: as x get large, y gets smaller

Example 3 - An increasing Exponential Function with an irrational exponent Increasing Functions: as x get large, y gets larger also

Example 4 - A decreasing (i.e. The coefficient of x is negative or b less than 1) Exponential Function with a rational exponent Decreasing Functions: as x get large, y gets smaller

Simplifying Irrational Exponents

Example 5. Simplify Remember: So

Example 6. Simplify Remember: So

Graphing Exponential Functions

Things to Know: (1) Increasing Exponential Function when either b is > 1 or the coefficient of x is positive (2) Decreasing Exponential Function when either b is < 1 or the coefficient of x is negative (3) The y-intercept is the coefficient of b, in most cases 1, so if , the y-intercept is (0, a) (4) When , the y-intercept is (0, 1) (5) The graph has a horizontal asymptotes at y = 0 (6) Domain is and Range is

Example 7 - Graph 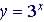First Create Table of Values x (x, y) -3 1/27 (-3, 1/27) -2 1/9 (-2, 1/9) -1 1/3 (-1, 1/3) 0 1 (0, 1) 1 3 (1, 3) 2 9 (2, 9) 3 27 (3, 27)

Graph

Example 8 - Graph 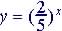First Create Table of Values x (x, y) -3 125/8 (-3, 125/8) -2 25/4 (-2, 25/4) -1 5/2 (-1, 5/2) 0 1 (0, 1) 1 2/5 (1, 2/5) 2 4/25 (2, 4/25) 3 8/125 (3, 8/125)

Graph

Compound Interest

Given: P as the principal or original deposit, r as the annual interest rate, t as the number of years and n as the number of times each year the balance is compounded (or is the principal plus the interest). Then the principal plus the compound interest is given by the formula: , Sometimes A is called the Future Value (FV) or the principal at time t. Continuous Compounding uses the formula: , where Often or the principal at time, t=0, the balance before any interest is earned or added. This P0 is called the present value (PV). Compound Interest: When interest is compounded for various periods each year the value of n reflect that compounding: Compound Period Value for n yearly 1 semiannually 2 quarterly 3 monthly 12 daily 365

Example 9. What will be the balance in a account after 6 years if the original balance was $20,000 and the account earned 5.25%, compounded yearly? Given: yearly compounding - so n = 1, P = $20,000, rate r = 5.25/100 = 0.0525 and t = 6 years. Formula is , So So balance after 6 years is $27,187.08	Example 10. How much interest would $10,000 earn in 5 years if compounded monthly at an annual rate of 6%? Given: monthly compounding - so n = 12, P = $10,000, rate r = 6/100 = 0.06 and t = 5 years Formula is = P + I (principal plus interest), so I, interest is found by I = Pt - P0 = Pt - 10000 So I = 13488.50 - 10000 = 3488.50 So interest is $3,488.50
Example 11. How much will $125,000 be worth in 25 years if compounded daily at nominal rate of 3.5% each year? Given: daily compounding - so n = 365, P = $125,000, rate r = 3.5/100 = 0.035 and t = 25 years. Formula is , So = 299846.83 So balance after 25 years is $299,846.83	Example 12. How much will $125,000 be worth in 25 years if compounded continuously at an annual rate of 3.5% each year? Given: continuous compounding - so n = big, P = $125,000, rate r = 3.5/100 = 0.035 and t = 25 years. Formula is So So balance after 25 years is $299,859.41

Transformation fo Exponentials

(Vertical and Horzontal shifts)

Given the exponential function 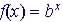Horizontal transformation occurs when h is introduced in the function in this manner: , when h is positive the functions is shifted to the right by h units and : when h is negative, the functions is shifted to the left by h units Vertical transformation occurs when k is introduced in the function in this manner: , when k is positive the functions is moves upward by k units and : when k is negative the function moves down by k units