Chapter  2.5 Proportion and Variation

Pindling College Algebra   by Example  Series

Key Concept: Understand proportionality and how to use it to define and solve applicable problems.

Skills to Learn:

1. Know the definition of a proportion and ratio

2. Know how to setup and solve simple proportional problems

3. Know how to recognize and solve direct proportional problems

3. Know how to recognize and solve inverse proportional problems

3. Know how to recognize and solve joint proportional problems

3. Know how to recognize and solve combine proportional problems

Definitions

Concepts	Examples and Illustrations
Ratio is the quotient of two numbers or identities.
Proportion is an equation setting two ratios equal to each other.
Direct Proportional (Direct Variation) occurs when the ratio of two variables or quantities or identities is a constant, k (k is a constant) k is the constant of proportionality	Example: The distance traveled, d in a given time, t varies directly with the speed, s (average speed is a constant, k). So the ratio of distance to time is a constant, speed (k) (mph is miles per hours)
Inverse Proportional (Inverse Variation) occurs when the product of two variables or quantities or identities is a constant, k. (k is a constant)	Example: The number of men it takes, N to complete a job is inversely related to the time it takes to do the job, t. So the product of number of men and time is a constant (k): If 30 men does the job in 2 hours, k = (30) x (2) = 60
Joint Proportional - occurs when you have 2 or more variables directly proportional to another variable. (k is a constant) Combine Proportional - occurs when variables are related directly and inversely to each other. (k is a constant)	Joint Proportionality: In 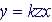(k is a constant), y varies directly with x and z Combine Proportionality: In (k is a constant), y varies directly with z and inversely with x.

Simple Proportionality Problems:

Notes: To solve the unknown quantity in a proportional statement it is best to rewrite the equation so as to isolate that quantity; for example let solve for x below: For any proportion , a and d are called the extremes and b and c are called the means and The product of the extremes = the product of the means (i.e. ). This is often called the cross-products.

Example - Solve for x in: Take cross products: , then expand , So

Example - Simplify without ratio: Take cross products:

Proportionality Example via applications

Example (Directly proportional): The circumference of a circle, C is directly proportional to the diameter of the circle, d.
If when the radius is 3 the circumference is 18.85, find

(a) The constant of proportionality, k

(b) Write the function that relates C to d and

(c) What is the diameter when the circumference is 100?

(a) find k, if or Given: C = 18.85 and r = 3 so d = 2(r) = 6 Since , So k = 3.142 (b) Since k = 3.142, the formula is (c) Since Since r = d / 2, r = 31.83 / 2 = 15.91

A graph of C = f(d) is:

Example (Inverse proportional): The N is inversely proportional to the square of x and when x = 2, N = 50.
What is N when x = 5?

First find k, if or Given: N = 50 and x = 2 So So k = 200 Since k = 200, then So

A graph of

Example (Joint Proportional): The power, in watts, dissipated as heat in a resistor varies jointly with resistance (R), in ohms, and the square of the current (I2), in amps. If a 10-ohm resistor with a current of 2 amps dissipates 40 watts how much power is dissipated in a 5-ohm resistor carrying a current of 3 amps? Find k from relationship of power, P: Given P = 10, R = 10, I = 1, so and So P = 45 watts ( k = 1)

Example (Combine Proportional): According to the Gas laws, the volume of a gas varies directly with the temperature, T and inversely with the pressure, P. When the temperature of a certain gas is 3300, the pressure is 40 pounds per square inch (psi) and the volume is 20 cubic feet. Find the volume when the pressure is 30 ppi and the temperate is 2800. Find k from relationship of volume, V: Given V = 20 ft3 , P = 40 psi , and T = 3300 So V = 22.62626262... ft3