Chapter
2.3 Writing Equations
of Lines
College Algebra
by Example Series
|
Chapter
2.3 Writing Equations
of Lines
|
College Algebra by Example Series |
Key Concepts: Given appropriate information about the graph of a line be able to write a suitable equation or formula for that graph.
Skills to Learn:
1. Know how to write an equation of a line given information in its point-slope format
2. Know how to write an equation of a line given its slope-intercept information
3. Know some basic applications of straight-line graphs such as depreciation
Equations of a line: Its various forms
| Forms of the Equation | Equations | Information Given |
|
Point-Slope |
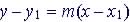
Example:
|
1. The slope, m
2. A point on the line ( Example: m = 4, P(-1, 4) |
|
Slope-Intercept |
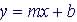, where b is y-intercept or y when x = 0
Example:
|
1. Information to find the slope,
m
2. The y-intercept, (0, b) |
|
Standard or General |
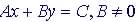
Example:
|
1. Usually, A, B, C are given
and equation needs rearranging or
2. Above 2 forms expanded |
Examples of various forms of equation of a line:
Problem 1: Find the equation of a line with slope - ½ that passes through the point (5,3).
| Information given is in the
slope-point format:
Given, m = - ½ and a point (5, 3) = So equation of the line is:
|
To Convert this to slope-intercept
format we need to find b, the y-intercept since the slope,
m is already given.
Slope-intercept form: To find b, let x = 0 and slope equation (1)
So Slope-intercept
|
| To get the standard form we expand
and rearrange equations (1) or (2) to get:
(1)
(2)
|
Graphs looks like:
|
Problem 2: Write an equation of the line that is parallel to 
that passes through the point (-8, - 6).
| Information given is in the
slope-point format
Since the slope m = 4, parallel to given line Given, m = 4 and a point (-8, - 6) = So equation of the line is:
|
To Convert this to slope-intercept
format we need to find b, the y-intercept since the slope,
m is already given.
Slope-intercept form: To find b, let x = 0 and slope equation (1)
So Slope-intercept
|
| To get the standard form we expand
and rearrange equations (1) or (2) to get:
(2)
|
Graphs looks like:
|
Problem 3: Write an equation of the line that is perpendicular
to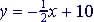 
that passes through the point (0, -20).
Information given is in the
slope-intercept format since the slope m is the negative recirpocal
of -½ (perpendicular line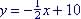
).
Given, So equation of the line is: Slope-intercept form:
|
To Convert this to slope-point
format we let m = 2, using point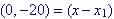 
we get
Slope-point:
Slope-intercept
|
| To get the standard form we expand
and rearrange equations (1) or (2) to get:
(2)
(2) |
Graphs looks like:
|
Problem 4: Find the equation of the line with these two points: (-2, 3) and (4, 6)
| First
we find the slope, m (see 2.2 Slope).
Given, (-2, 3) = So
Slope-point: Using (4, 6) is
The y-intercept is y when x =0,
Slope-intercept form:
|
Graphs looks like:
|
Problem 5: The value of an office equiptment depreciates in value from $35,000 to $4,500 in 7 years:
(a) Write the equation of a line if the depreciation is linear
(b) What is the meaning of m in this equation?
(c) What was the value of the equipment after 5 years?
| If we let the start time of
the depreciation be t = 0, where t is time in years, then b = $35,000; i.e.
The value of the equipment when t = 0.
So given 2 points: (0, 35000) and (7, 4500)
Next find the slope, m
(a) So slope-intercept (V = mt + b) form is
The slope-point form is:
Using (7, 4500)
(b) m = -142.86, means that the value of the equipment decrease by $4,357.14 each year. |
Graphs looks like:
(c) After 10 years, t = 5 using (1), V =
|
, m = ½ and b =-2
=
(1)
(2)
or
(3)
(3)
.
=
(1)
(2)
(3)
and from the point (0, -20),
(1)
or
(2)
(3)
and 
(1)
(2)
(1)
(2)
