College Algebra Home
Chapter 1.7 Inequalities
Pindling
College Algebra  
by Example  Series

Key Concept: Understand the relative positioning of numbers as functions of inequalities with respect to points on the number line.:

Skills to Learn:

1. Use properties of inequalities to interpret any real numbers or the domain of functions on the number line. (e.g. )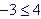

2. Know how to solve linear inequalities. (e.g. )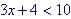

3. Know how to solve compound inequalities (e.g. )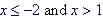

4. Know how to solve quadratic inequalities (e.g. )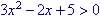

5. Know how to solve rational inequalities.(e.g. )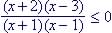

Illustrated Inequalities Table:

Symbol Description Example Illustration

Not equal to

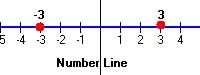
< or

)

Less than

1 < 3

or

]

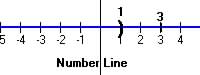
Less than or equal to

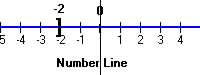
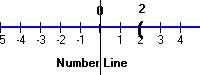
> or

(

Greater than

2 > 0

or

[

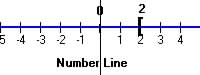
Greater than or equal to

Approximately equal to

Examples - General Inequalities Properties

Property If a,b and c are real numbers

Property If a,b,c and n are real numbers

(a) If a < b and b < c, then a < c

If 2 < 4 and 4 < 12, then 2 < 12

 (e) If a < b and c > 0, then ca < cb

If 3 < 8 and c = 2 (2 > 0), then 2(3) < 2(8)

(i.e. 6 < 16)
(b) If a > b and b > c, then a > c

If 12 > 10 and 10 > 8, then 12 > 8

 (f) If a < b and c > 0, then

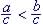
If 3 < 8 and c = 2, then

(c) If a < b, then a + c < b + c

If 3 < 5, then 3 + 6 < 5 + 6 (9 < 11)

 (e) If a < b and c < 0, then ca > cb

If 3 < 8 and c= -2, then -2(3) > -2(8)

(i.e. -6 > -16)
(d) If a > b, then a - c > b - c

If 5 > 3, then 5 - 2 > 3 -2 (3 > 1)

 (e) If a < b and c < 0, then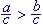

If 2 < 8 and c = -2, then (i.e. -1>-4)

Examples - Linear Inequalities

Example 9. Solve

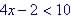
Add -2 to both sides

(divide by 4)




Check:

Example 10. Solve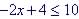

Subtract 4 from both sides

(divide by -2, note )

Check:

Example 11. Solve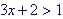

Subtract 2 from both sides

(divide by 3)




Check

Example 12. Solve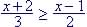

Multiply both side by common multiple, 6

group terms

(multiply by -1)

(note )




Check

Examples - Quadratic Inequalities

Example 13 Solve

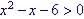
(also compound inequalities)

1. First solve (=):

So and

2. Establish intervals (after arranging solutions in order):




3. Test a value within each interval (domain) to see if equation is true.

Test 1

So True

Test 2

, Not True

Test 3

So True

4. State Answer: The solutions are in the intervals

Example 14 Solve

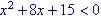
(also compound inequalities)

1. First solve (=):

So

2. Establish intervals (after arranging solutions in order):




3. Test a value for each domain:

Test 1

, Not True

Test 2

, True

Test 3

, Not True

4. State Answer: The solutions are in the interval

Example 15 Solve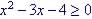

(also compound inequalities)

1. First solve (=):

So

2. Establish intervals (first order solutions)

3. Test a value within each domain

Test 1

, True

Test 2

, Not True

Test 3

, True

4. State Answer: The solutions are in the intervals

Example 16 Solve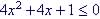

1. First solve (=):

So 2x + 1 = 0, x = - ½

2. Establish intervals (note solution is one value of - ½ )




3. Test the value x = - ½

Test 1

True

Note other values of x are not true

Test 2: we get

Test 3: x = 2 we get

4. State Answer: The only solution is x = - ½

Rational Inequalities

Example 17. Solve

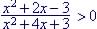
1. First solve (=): and

(a) numerator: , so x=1 & -3

(b) denominator.: , so x= -1 & -3

2. Establish intervals (first order solutions)




3. Test a value within each domain

Test 1:

, True

Test 2:

, True

Test 3:

, Not True

Test 4:

, True

4. State Answer: The solutions are in the intervals:

Example 18. Solve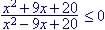

1. First solve (=): and

(a) Numerator: , so x = -4, -5

(b) Denominator: , so x = 4, 5

2. Establish intervals (first order solutions)




3. Test a value within each domain

(since x = -4 and -5, so ] or [ in solution)

Test 1:

, False

Test 2:

, True

Test 3:

, False

Test 4:

, True

Test 5:

, False

4. State Answer: The solutions are in the intervals:
Example 19. Solve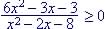

1. First solve (=): and

(a) numerator: , so x =1,- ½

(b) denominator: , so x =4, -2

2. Establish intervals (first order solutions)




3. Test a value within each domain

Test 1:

, True

Test 2:

, False

Test 3:

, True

Test 4:

, True

Test 5:

, True

4. State Answer: The solutions are in the intervals:

 Example 20. Solve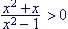

1. First solve (=): and

(a) numerator: x = 0 and -1

(b) denominator: x = -1 and 1

2. Establish intervals (first order solutions)




3. Test a value within each domain

Test 1:

, True

Test 2:

, True

Test 3:

, Not True

Test 4:

, True

4. State Answer: The solutions are in the intervals: