Chapter 1.6 Polynomial and radical Equations

Pindling College Algebra   by Example  Series

Key Concept: Using a principle of power or second degree of polynomials solve other degrees polynomials and radicals:

If a and b are real numbers, n is an integer, and a = b, then

Skills to Learn:

1. How to factor polynomials by grouping powers of n.

2. How to solve radical equations by first eliminating the radical.

4. Check that answers are consistent with problem statement(s).

Example 1. Solve for x in the following: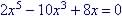

Traditional Method First factor common factor, 2x Factor , note , Remember Then So: 2x = 0 or x = 0 x = -2 x = 2 x = -1 x = 1	Substitution Method First factor common term, 2x Substitute s = x2, then s2 =x4 Replace s with x2 Then So x = 0, -2, 2, -1 and 1
Graphical Method - cannot be used in this course (note x = -2, -1, 0, 1 and 2 when y =0)	Checks: Answers checked

Example 2. Solve for x in the following: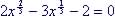

Traditional Method Factor of the form , where absolute value of a, b are either 2 or 1 So So: and	Substitution Method Substitute Replace Solve as traditional and
Graphical Method - cannot be used in this course	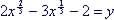Checks: Answers checked

Radical Equations: Strategy Remove the radical by using power or exponent properties

Example 3. Find all real solution to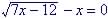

Solution Rearrange so radical is on one side of equation (now square both sides to remove radical) , so , or (note rearrange so coefficient of x2 is +) Factor quadratic to get Possible solutions are x = 3 and 4

Check Squaring both sides of an equation may introduce extraneous roots, so check each answer to see if valid. Checks Checks So x = 3 and 4

Example 4. Find all real solution to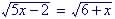

Solution Remove radicals by squaring both sides , so group like terms and solve A possible solution is x = 2

Check Squaring both sides of an equation may introduce extraneous roots, so check each answer to see if valid. Checks So x = 2

Example 5. Find all real solution to

Solution Remove radicals by raising both sides to the power of 3 , A possible solution is x = 12

Check Squaring both sides of an equation may introduce extraneous roots, so check each answer to see if valid. Checks So x = 12

Example 6. Find all real solution to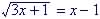

Solution Remove radicals by raising both sides to the power of 2 , group like terms and write as quadratic (factored out common term x) Possible solutions are x = 0, 5

Check Squaring both sides of an equation may introduce extraneous roots, so check each answer to see if valid. Invalid Result Checks So x = 5 is only valid answer