
College Algebra
by Example Series

Chapter
1.2 Applications of Linear Equations
|
College Algebra by Example Series |
Problem Solving Strategy (Polya)
1. Understand the problem
2. Devise a plan (or strategy)
3. Carry out the plan
4. Check back
Purpose of Section: To learn problem solving by examples of linear equations.
The Linear Formula / Model
A linear formula is of the form: 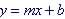 , where x and y are variables, m is the slope of the line or the rate of
change of the function and b is the value of the function when x =0.
, where x and y are variables, m is the slope of the line or the rate of
change of the function and b is the value of the function when x =0.
Example 1. Average Problem - The average of 5 students in a class is 85%, if 4 students have a score of 75%, 80%, 82% and 90%, what is the score of the 5th student?
Problem Solving Strategy:
| 1. Understand the problem | Average is the sum of all scores
divided by the total number of scores, n = 5.
Since the average of all scores is 85% then there we need to find the unknown score, so let the score of the 5th student be called x (unknown). Find x. |
| 2. Devise a plan | Using the formula of average (Ave.) and the knowledge that there is only
one unknown, x we can setup the problem to solve for x:
Find x. |
| 3. Carry out the plan. | Solve for x by simple algebra:
Next add all numbers on left side of equation to get 327 + x = 425 (next subtract 327 to both sides to isolate x) So x = 98 or 98% (note that % is the unit of the numbers being averaged) |
| 4. Check back | Check that when
x = 98 the original problem statement in statement 2 is true or
correct:
So answer checks |
Example 2 - Perimeter Problem
- If the perimeter around a rectangular swimming pool is 100 feet and the
length
of pool is 50% more than the width. Find the length and width of the pool.
| 1. Understand the problem | Since the perimeter of a rectangular
object or figure is equal to twice the length, L plus twice the width, W then
if we know the perimeter and can relate to width to the length; i.e. Length
= Width + 50% of Width.
We must remove the % sign by converting % to its decimal equivalence. So 50% is the same as 0.5. Therefore L = W + 0.5W. Know that Perimeter = 2L + 2W = 100 feet (Given) Find L and W. |
| 2. Devise a plan | Using 2 sets of information:
1. Perimeter = 2L + 2W = 100 and 2. L = W + 0.5W
We can replace L with W + 0.5W to have a simple linear equation to find W then using equation 2 find L. Find W first then L. |
| 3. Carry out the plan. | Replace L = W + 0.5W in equation 1 and
solve for W.
So Perimeter = 2(W + 0.5W) + 2W = 100 (expand)
2W + W + 2W = 100 (group like terms) 5W = 100, so W = 100/5 = 20 Find L given that W = 20 by using equation 2. L = W + 0.5W = 20 + 0.5(20) = 20 + 10 = 30 So Width, W = 20 feet and Length, L = 30 feet |
| 4. Check back | Check equation 1 to see if W = 20 and L
= 30 gives a percent of 100
(1) Perimeter = 2L + 2W = 100 2(30) + 2(20) = 60 + 40 = 100 This answer checks |
Example 3 - Investment Problem
- Part of $25,000 was invested at a rate of 10% and the rest at a rate of
16%.
If the interest from these investments were $3,200, how much was invested
at each rate?
| 1. Understand the problem | Since involve annual interest,
know that interest equal amount invested times the rate (decimal equivalent
to the %).
Let amount invested at 10% be x, so amount invested at 16% would be equal to $25,000 - x. So if find x can also find rest ($25,000 - x) Find x, amount invested at 10% and use it to find rest. |
| 2. Devise a plan | Since the total interest is $3,000, clearly
this is based on the sum of the interest gain from both investments.
So total interest, I = Interest from 10% + Interest from 16% (convert % to their decimal equivalencies - 16% is same as 0.16 etc.) Interest from 10% = 0.1 times x and interest from 16% = 0.16 times (25,000 - x) or I = 3,200 = 0.1(x) + 0.16(25000 - x) Find x, 10% investment then 25,000 - x, 16% investment |
| 3. Carry out the plan. | Solve for x using the formula devised above.
I = 3200 = 0.1x + 0.16(25000 - x) - expand 3200 = 0.1x + 4000 -.16x (group terms) 3200 - 4000 = 0.1x - 0.16x, -800 = -0.06x 0.06x = 800, so x = $13333.33
If x = $13,333.33, then rest = 25000 - x = $11,666.67 |
| 4. Check back | Check that x = 13,333.33 give I = 3200
I = 3200 = 0.1(13333.33) + 0.16(25000 - 13333.33) = 1333.33 +1866.67 = 3200 So this answer checks |
Example 4 - Break Even Point Problem
- Find the break even point for a business if its expense to operate includes
a setup cost of $5,000 with a unit cost of $2.50 and its revenue is equal
to $1,000 with an increase of $5 for each unit sold.
| 1. Understand the problem | Break even point is the point
at which two forces equal or two equations equal or for this problem the expense
= the revenue.
So we need to find a formula for both the expense and revenue and then determine how many units need to be sold so that the business breaks even; expense = revenue. Find x, the number of units so that expense = revenue. |
| 2. Devise a plan | Let x be number of units sold then:
Expense, E = $5000 + 2.50x (setup cost + cost for each units made) Revenue, R =$1000 + $5x (initial profit + revenue each unit sold) Let R = E or 5000 + 2.5x = 1000 + 5x Find x, that makes R = E |
| 3. Carry out the plan. | Solve for x that satisfy R = E
Find x when: 5000 + 2.5x = 1000 + 5x (group terms) 5000 - 1000 = 5x - 2.5x, 4000 = 2.5x, So x = 4000 / 2.5 = 1600 units
|
| 4. Check back | Check that when x = 1600, R = E
R = 5000 + 2.5(1600) = 9000 E = 1000 + 5(1600) = 9000 So R = E when x = 1600, So this answer checks |
Example 5 - Mixture Problem
- A winery must mixed two grades of wine to obtain a final mixture of 11%
alcohol.
If it has 25 gallons of 15% percent alcohol in a drum, how much 8% alcohol
must be added to achieved the desired end?
| 1. Understand the problem | The sum of the two alcohol
mixtures must equal the final alcohol content of 15%.
So alcohol in 8% mixture + alcohol in 15% mixture = 11% alcohol mixture. Let the amount of 8% alcohol to be added be equal be x, then the total volume of the final mixture is 25 gallons + x; this must be 11% alcohol. Find x, the number of gallons of 8% alcohol to be added to the 25 gallon 15% mixture. |
| 2. Devise a plan | So setup relationships between the two
mixture and the final outcome and solve for x.
8% of x + 15% of 25 gallons = 11 % of final mixture Write as a mathematical relationship and solve for x. (convert % to decimal equivalent) 0.08x + 0.15(25) = 0.11(25 + x) Find x, that makes R = E |
| 3. Carry out the plan. | Solve for x
0.08x + 0.15(25) = 0.11(25 + x) expand 0.08x + 3.75 + = 2.75 + 0.11x (group terms) 0.08x - 0.11x = 2.75 - 3.75, -0.03x = - 1 So x = 1 / 0.03 = 33.33 gallons
|
| 4. Check back | Check that when x = 33.33 gallons we get
a 11% alcohol mixture
So total mixture is 25 + 33.33 gallons = 58.33 gallons Final mixture's alcohol content is 15% of 25 gallons + 8% of 33.33 gallons = 0.15(25) + 0.08(33.33) = 6.4167 gallons Alcohol content of final mixture is 6.4167 / 58.33 = 0.11 or 11% So this answer checks |
Example 6 - Uniform Motion Problem
- Object A believes it is faster than object B. If object A gives object B
a
head start in a race of ½ hour and object A moves at an average speed
of 10 miles per hour and object B moves at
an average speed of 8 mph. Will Object A pasts Object B in 3 hours? (assume
that the time it takes each to reach
average speed is negligible).
| 1. Understand the problem | Speed, s is distance travel,
d divided by the time, t it takes to travel that distance. 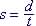
However if one can find the time it takes for both object to be at the same point (distance), then after that time of distance the faster object would be at an advantage. So time is speed times distance or Find the t for both to catch up and see if it is before 3 hours. |
| 2. Devise a plan | Find formulas for the distance both objects
traveled and solve for t in hours, the time it takes to catch up.
So distance object A traveled is 10(t) = 10t Distance object B traveled is 8(t + ½ ) - head start of ½ hour. To find when they catch-up set these two equations equal to each other and solve for t. Find t and see if it is greater than 3 hours. |
| 3. Carry out the plan. | Solve for t
When 10t = 8(t + ½ ) 10t = 8t + 4 (group terms) 10t - 8t = 4, so 2t = 4 and t = 2 hours
So they catch up 2 hours after the race starts, so object A will win the 3 hour race.
|
| 4. Check back | Check that x = 2 satisfies the equation
above.
10(2) = 8(2 + ½ ) = same = 20 miles (speed x time) So this answer checks |