Chapter 1.1. Equations

Pindling College Algebra   by Example  Series

Is x = b? (true or false?), x is called a variable and can assume any value.

3 Possible Outcomes:

1. Identity: Every possible values of x is true

For example, sin² x + cos² x = 1, this is true for all real values of x.

Many solutions so many roots.

2. Impossible equations or solutions (Contradictions) - no solution:

For example, x = x + 2, no real number is a solution.

Also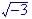

No solution so no root.

3. Conditional solutions or equations:

For example, 3x + 1 = 7, only one or few values of x satisfies the equation,

here x = 2.

One or few solutions or root(s).

Summary of Types of Equations:

Identity	Conditional	No Solution
Property: Both sides of the equations are the same	One or more solutions when solving for the variable	No real solutions exist
Key Examples 1. 3(x + 3) = 3x + 9 2. 23 = 8 3. x2 + 5x + 6 =(x + 3)(x + 2)	Examples: 2x + 1 > 0, any value of  x > -½ (x + 1)(x - 3) = 0,  x = -1 ans 3	1. = x 2.